I. Introduction▲
Plongeons-nous dans l'univers de la reconnaissance de formes. Plus particulièrement, nous allons nous intéresser à la reconnaissance des chiffres (0, 1, ..., 9). Imaginons un programme qui devrait reconnaître, depuis une image, un chiffre. On présente donc au programme une image d'un "1" manuscrit par exemple et lui doit pouvoir nous dire "c'est un 1". Supposons que les images que l'on montrera au programme soient toutes au format 200x300 pixels. On aurait alors 60000 informations à partir desquelles le programme déduirait le chiffre que représente cette image. L'utilisation principale des réseaux de neurones est justement de pouvoir, à partir d'une liste de n informations, pouvoir déterminer à laquelle des p classes possibles appartient cette liste.
De façon plus générale, un réseau de neurone permet l'approximation d'une fonction. Ici, il s'agit d'une fonction de classification : à chaque n-uplet d'informations en entrée la fonction associe une classe.
Dans la suite de l'article, on notera kitxmlcodeinlinelatexdvpX = (x_{i})_{1 \leq i \leq n}finkitxmlcodeinlinelatexdvp un vecteur dont les composantes sont les n informations concernant un exemple donné. Dans l'exemple de la reconnaissance de formes, un exemple est une image représentant plus ou moins approximativement un chiffre. C'est un objet descriptible par n informations. De plus, on notera C1, C2, ..., Cp les p classes. Dans l'exemple précédent, les classes correspondent aux chiffres.
Voyons maintenant d'où vient la théorie des réseaux de neurones artificiels.
II. Une origine... biologique !▲
Comment l'homme fait-il pour raisonner, parler, calculer, apprendre... ? Comment s'y prendre pour créer une intelligence artificielle ? Deux types d'approches ont été essentiellement explorées :
- procéder d'abord à l'analyse logique des tâches relevant de la cognition humaine et tenter de les reconstituer par programme. C'est cette approche qui a été privilégiée par l'Intelligence Artificielle symbolique et la psychologie cognitive classiques. Cette démarche est étiquetée sous le nom de cognitivisme.
- puisque la pensée est produite par le cerveau ou en est une propriété, commencer par étudier comment celui-ci fonctionne. C'est cette approche qui a conduit à l'étude des réseaux de neurones formels. On désigne par connexionnisme la démarche consistant à vouloir rendre compte de la cognition humaine par des réseaux de neurones.
La seconde approche a donc mené à la définition et à l'étude de réseaux de neurones formels qui sont des réseaux complexes d'unités de calcul élémentaires interconnectées. Il existe deux courants de recherche sur les réseaux de neurones : un premier motivé par l'étude et la modélisation des phénomènes naturels d'apprentissage pour lequel la pertinence biologique est importante ; un second motivé par l'obtention d'algorithmes efficaces ne se préoccupant pas de la pertinence biologique. Nous nous plaçons du point de vue du second groupe. En effet, bien que les réseaux de neurones formels aient été définis à partir de considérations biologiques, pour la plupart d'entre eux, et en particulier ceux étudiés dans ce cours, de nombreuses caractéristiques biologiques (le temps, la mémoire...) ne sont pas prises en compte. Toutefois, nous donnons, dans la suite de cette introduction, un bref aperçu de quelques propriétés élémentaires de neurophysiologie qui permettent au lecteur de relier neurones réels et neurones formels. Nous donnons ensuite un rapide historique des réseaux de neurones.
La physiologie du cerveau montre que celui-ci est constitué de cellules (les neurones) interconnectées. Les principales étapes de cette découverte sont :
- Van Leuwenhook (1718) : première description fidèle de ce qu'on appellera plus tard les axones ;
- Dutrochet (1824) : observation du corps cellulaire des neurones ;
- Valentin : découverte des dendrites ;
- Deiters (1865) : image actuelle de la cellule nerveuse ;
- Sherington (1897) : les synapses ;
- les neuro-transmetteurs (première moitié du 20ème siècle).
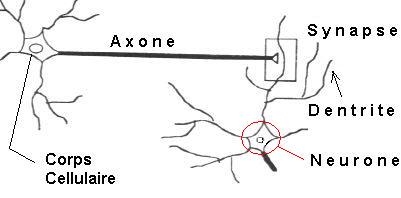
Les neurones reçoivent les signaux (impulsions électriques) par des extensions très ramifiées de leur corps cellulaire (les dendrites) et envoient l'information par de longs prolongements (les axones). Les impulsions électriques sont régénérées pendant le parcours le long de l'axone. La durée de chaque impulsion est de l'ordre d'1 ms et son amplitude d'environ 100 mV.
Les contacts entre deux neurones, de l'axone à une dendrite, se font par l'intermédiaire des synapses. Lorsqu'une impulsion électrique atteint la terminaison d'un axone, des neuromédiateurs sont libérés et se lient à des récepteurs post-synaptiques présents sur les dendrites. L'effet peut être excitateur ou inhibiteur.
Chaque neurone intègre en permanence jusqu'à un millier de signaux synaptiques. Ces signaux n'opèrent pas de manière linéaire : il y a un effet de seuil.
Voici quelques informations à propos des neurones du cerveau humain :
- le cerveau contient environ 100 milliards de neurones.
- on ne dénombre que quelques dizaines de catégories distinctes de neurones.
- aucune catégorie de neurones n'est propre à l'homme (cela serait trop beau !).
- la vitesse de propagation des influx nerveux est de l'ordre de 100m/s, c'est à dire bien inférieure à la vitesse de transmission de l'information dans un circuit électronique.
- on compte de quelques centaines à plusieurs dizaines de milliers de contacts synaptiques par neurone. Le nombre total de connexions est estimé à environ 1015.
- la connectique du cerveau ne peut pas être codée dans un "document biologique" tel l'ADN pour de simples raisons combinatoires. La structure du cerveau provient donc en partie des contacts avec l'environnement. L'apprentissage est donc indispensable à son développement.
- le nombre de neurones décroit après la naissance. Cependant, cette affirmation semble remise en question.
- on observe par contre une grande plasticité de l'axone, des dendrites et des contacts synaptiques. Celle-ci est surtout très importante après la naissance (on a observé chez le chat un accroissement des contacts synaptiques de quelques centaines à 12 000 entre le 10ème et le 35ème jour). Cette plasticité est conservée tout au long de l'existence, bien qu'affaiblie lors du processus de vieillesse ; on parle alors de "rigidité synaptique".
- les synapses entre des neurones qui ne sont pas simultanément actifs sont affaiblis puis éliminés.
- il semble que l'apprentissage se fasse par un double mécanisme : des connections sont établies de manière redondantes et aléatoires puis seules les connexions entre des neurones simultanément actifs sont conservés (phase de sélection) tandis que les autres sont éliminés. On parle de stabilisation sélective.
III. Un neurone seul▲
Un neurone est, comme vous l'avez vu, l'unité élémentaire de traitement d'un réseau de neurones. Il est connecté à des sources d'information en entrée (d'autres neurones par exemple) et renvoie une information en sortie. Voyons comment tout cela s'organise.
III-1. Entrées▲
On note (xi)1 <= i < k les k informations parvenant au neurone. De plus, chacune sera plus ou moins valorisée vis à vis du neurone par le biais d'un poids. Un poids est simplement un coefficient wi lié à l'information xi. La i-ème information qui parviendra au neurone sera donc en fait wi*xi. Il y a toutefois un "poids" supplémentaire, qui va représenter ce que l'on appelle le coefficien de biais. Nous le noterons w0 et le supposerons lié à une information x0 = -1. Nous verrons plus tard son utilité, dans la section Fonction d'activation.
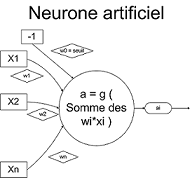
Le neurone artificiel (qui est une modélisation des neurones du cerveau) va effectuer une somme pondérée de ses entrées plutôt que de considérer séparément chacune des informations. On définit une nouvelle donnée, in, par :
kitxmlcodelatexdvpin = \sum_{i = 0}^{k}w_{i} \times x_{i} = (\sum_{i = 1}^{k}w_{i} \times x_{i}) - w_{0}finkitxmlcodelatexdvpC'est en fait cette donnée-là que va traiter le neurone. Cette donnée est passée à la fonction d'activation, qui fait l'objet de la prochaine section. C'est d'ailleurs pour ça que l'on peut parfois appeler un neurone une unité de traitement.
III-2. Fonction d'activation▲
La fonction d'activation, ou fonction de transfert, est une fonction qui doit renvoyer un réel proche de 1 quand les "bonnes" informations d'entrée sont données et un réel proche de 0 quand elles sont "mauvaises". On utilise généralement des fonctions à valeurs dans l'intervalle réel [0,1]. Quand le réel est proche de 1, on dit que l'unité (le neurone) est active alors que quand le réel est proche de 0, on dit que l'unité est inactive. Le réel en question est appelé la sortie du neurone et sera noté a. Si la fonction d'activation est linéaire, le réseau de neurones se réduirait à une simple fonction linéaire.
En effet, si les fonctions d'activations sont linéaires, alors le réseau est l'équivalent d'une régression multi-linéaire (méthode utilisée en statistiques) . L'utilisation du réseau de neurone est toutefois bien plus intéressante lorsque l'on utilise des fonctions d'activations non linéaires.
En notant g la fonction d'activation, on obtient donc la formule donnant la sortie d'un neurone :
kitxmlcodelatexdvpa = g(in) = g(\sum_{i = 0}^{k}w_{i}\times x_{i})finkitxmlcodelatexdvpRemarquez que le coefficient de biais est inclus dans la somme, d'où la formule plus explicite :
kitxmlcodelatexdvpa = g(in) = g((\sum_{i = 1}^{k}w_{i} \times x_{i}) - w_{0})finkitxmlcodelatexdvpIl y a bien sûr beaucoup de fonctions d'activations possibles, c'est à dire répondant aux critères que nous avons donnés, toutefois dans la pratique il y en a principalement 2 qui sont utilisées :
- La fonction de Heaviside
- La fonction sigmoïde
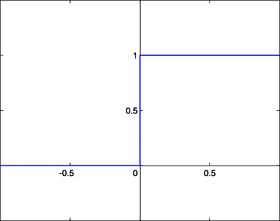
La fonction de Heaviside est définie par : kitxmlcodeinlinelatexdvp\forall x \in R, g(x) = 1finkitxmlcodeinlinelatexdvp si kitxmlcodeinlinelatexdvpx \geq 0finkitxmlcodeinlinelatexdvp, 0 sinon.
La fonction sigmoïde est quand à elle définie par : kitxmlcodeinlinelatexdvp\forall x \in R, g(x) = \frac{1}{1 + e^{-x}}finkitxmlcodeinlinelatexdvp
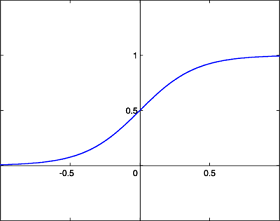
La fonction sigmoïde présente l'avantage d'être dérivable (ce qui va être utile par la suite) ainsi que de donner des valeurs intermédiaires (des réels compris entre 0 et 1) par opposition à la fonction de Heaviside qui elle renvoie soit 0 soit 1. Toutefois, les deux fonctions possèdent un seuil. Celui de la fonction de Heaviside est en x = 0 et vaut 1 alors que celui de la fonction sigmoïde est en 0 également mais vaut 1/2.
Revenons à notre neurone et demandons-nous quand est-ce que le seuil est atteint, ou dépassé dans le cas de la fonction sigmoïde. Il est dans tous les cas atteint quand in vaut 0.
kitxmlcodelatexdvpin = 0 \Leftrightarrow \sum_{i = 0}^{k}w_{i} \times x_{i} = 0 \Leftrightarrow (\sum_{i = 1}^{k}w_{i} \times x_{i}) - w_{0} = 0 \Leftrightarrow \sum_{i = 1}^{k}w_{i} \times x_{i} = w_{0} finkitxmlcodelatexdvpC'est là qu'intervient réellement le coefficient de biais. Nous voyons donc que l'on atteint le seuil de la fonction d'activation lorsque la somme pondérée des informations d'entrée vaut le coefficient de biais. De plus :
kitxmlcodelatexdvpin \geq 0 \Rightarrow g(in) \geq seuilfinkitxmlcodelatexdvpoù seuil vaut 1 si g est la fonction seuil, 0 si g est la fonction sigmoïde. Les propriétés énoncées ci-dessus sont vraies grâce à la croissance des fonctions d'activations.
Maintenant, notons W = (wi)1 <= i <= n le vecteur dont les composantes sont les poids et X = (xi)1 <= i <= n le vecteur dont les composantes sont les informations d'entrées du neurone. Avec cette notation on obtient : kitxmlcodeinlinelatexdvp W \cdot X = 0finkitxmlcodeinlinelatexdvp
Ceci définit un hyperplan d'un espace de dimension n. En fait, l'espace dont il est question est l'espace des informations d'entrées. De la même manière que dans notre monde nous décrivons des points avec nos 3 coordonnées souvent notées (x,y,z), dans l'espace des informations d'entrée on note les coordonnées (x1, ..., xn). Un hyperplan est un espace de dimension n-1. Dans notre monde, l'espace est de dimension 3 (car 3 coordonnées) et un hyperplan est donc un espace de dimension 2. En dimension 3, un hyperplan est donc simplement un plan. En dimension 2, un hyperplan est par conséquent une droite.
Plaçons-nous en dimension 2. Tracez donc 2 axes perpendiculaires. Maintenant, tracez une droite. Vous voyez que cette droite sépare le plan en 2 parties. A quoi cela sert-il ? En fait, un réseau de neurone simple (nous le verrons plus loin) va permettre de classer les points du plan dans une partie ou l'autre du plan grâce à cette droite, dans le cas de la dimension 2. Encore une fois, dans ce cas-là, ceux qui seront dans une partie du plan appartiendront à la première classe et ceux qui seront dans l'autre partie du plan (de l'autre côté de la droite) appartiendront à la deuxième classe.
III-C. Activation et condition d'activation▲
On dit que le neurone est actif lorsque in >= 0, autrement dit lorsque a = g(in) >= seuilg = g(0). Similairement, on dit que le neurone est inactif lorsque in <= 0, autrement dit lorsque a = g(in) <= seuilg = g(0).
III-D. Exemple en dimension 2 : la fonction booléenne OU▲
Dans ce cas, nous allons décrire une entrée par 2 informations. En effet, la fonction booléenne OU prend 2 informations en entrée (deux nombres qui peuvent valoir 0 ou 1 chacun) et retourne 1 si l'un des deux au moins vaut 1. Ici, nous allons grâce à un neurone simuler cette fonction, en rajoutant de la souplesse (en entrée nous accepterons des nombres réels compris entre 0 et 1).
Tout d'abord, il faut que nous-même sachions décrire le fonctionnement. Nous pouvons dire que le neurone pourra être actif lorsque w1x1 + w2x2 >= 0.5, ce qui représente la partie des réels entre 0 et 1 qui est la plus proche de 1. Nous avons donc déjà le seuil du neurone, qui sera ici 0,5. De plus, on peut considérer que si x1 = x2 = 0.25, le neurone renverra 1. On va donc finalement choisir comme poids w1 = w2 = 1 et comme nous l'avons dit, le coefficient de biais, aussi appelé seuil, w0 = 0.5.
Tracez les axes perpendiculaires puis la droite qui passe par les points (0.25,0) et (0,0.25). Tous les points qui se trouvent en-dessous de la droite seront ceux pour lesquels le neurone renverra 0, les autres seront ceux pour lesquels le neurone renverra 1.
En effet, prenons par exemple comme entrées le couple (0.1,0.8). Le calcul fait par le neurone est le suivant.
kitxmlcodelatexdvpin = 1 \times 0.1 + 1 \times 0.8 = 0.9 \geq 0.5finkitxmlcodelatexdvpdonc a = g(in) = 1.
Ainsi on remarque que le point (0.1,0.8) est un point pour lequel le neurone doit renvoyer la valeur 1 en sortie, car la somme pondérée des entrées est supérieure au seuil. Si l'on regarde sur le dessin contenant la droite séparatrice que vous avez tracé, on constate effectivement que ce point là se situe bien dans la zone supérieure du plan que délimite la droite.
Etant donné que la fonction OU renvoie 1 ou 0 généralement, et non pas un réel de [0,1], la fonction seuil suffira bien amplement pour notre neurone.
Nous avons ainsi entièrement déterminé notre neurone. Ainsi, ce neurone prend les mêmes valeurs que la fonction booléenne OU, ce qui constitue une approximation parfaite de cette dernière.
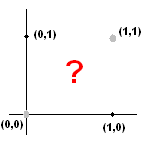
Maintenant, essayez de reproduire cette démarche pour la fonction XOR. La fonction booléenne XOR renvoie 1 quand l'une de ses deux entrées vaut 1, 0 sinon. Essayez donc de placer les points pour lesquels x XOR y vaut 1 en noir et ceux pour lesquels x XOR y vaut 0 en gris clair. Essayez maintenant de tracer une droite séparant les points noirs des points blancs. Vous verrez alors que c'est impossible. On voit donc les limitations du neurone seul. Qui plus est, le modèle de réseau de neurone qui va être étudié dans la partie qui suit ne permet pas non plus de représenter la fonction XOR, car il ne servira qu'à obtenir plusieurs sorties au lieu d'une seule, chaque neurone faisant sa partie du travail.
A titre informatif, le modèle qui vient d'être présenté est celui établi par McCulloch et Pitts en 1943. Nous allons justement dans la partie qui suit étudier le modèle du perceptron.
En résumé :
- Un neurone est l'unité élémentaire de traitement d'un réseau de neurones ;
- Un neurone est relié à chacune de ses informations et à chacune de ces liaisons est attaché un nombre réel, nommé poids ;
- Un neurone possède un seuil, qui est modélisé par une information de valeur -1 et un poids w0, où justement w0 est le seuil ;
- Un neurone ne traite pas chaque information indépendamment, mais effectue la somme des produits des informations par leur poids associé et traite cette donnée ;
- Il existe plusieurs fonctions de transferts remplissant les conditions nécessaires ;
- Quelle que soit la fonction de transfert, elle prendra l'image de la somme pondérée des informations, y compris le -w0 ;
- La fonction booléenne OU peut être approchée par un seul neurone. Il en est de même pour la fonction ET ;
- Une fonction de classification qui consiste en l'insertion d'un hyperplan séparant les points appartenant à une première classe de ceux appartenant à une seconde est approchable par un neurone seul ;
- Pour les fonctions pour lesquelles c'est impossible, il faut établir un réseau de neurones multicouche.
IV. Réseau de neurones monocouche : le perceptron▲
Un réseau de neurones monocouche, aussi appelé perceptron, est caractérisé de la manière suivante.
- Il possède n informations en entrée ;
- Il est composé de p neurones, que l'on représente généralement alignés verticalement. Chacun peut en théorie avoir une fonction d'activation différente. En pratique, ce n'est généralement pas le cas ;
- Chacun des p neurones est connecté aux n informations d'entrée.
Le réseau de neurones possède ainsi n informations en entrée et p sorties, chaque neurone renvoyant sa sortie.
Pour la suite, on notera :
- X = (xi)1 <= i <= n les n informations d'entrée ;
- wi,j pour 1 <= i <= n et 1 <= j <= p, le poids reliant l'information xi et le neurone j puis aj l'activation du j-ème neurone ;
- w0,j le coefficient de biais, également appelé seuil, du j-ème neurone ;
- inj la donnée d'entrée (somme pondérée) du j-ème neurone.
On a donc l'équation suivante :
kitxmlcodelatexdvp\forall 1 \leq j \leq p , a_{j} = g(in_{j}) = g(\sum_{i = 0}^{n}w_{i,j} \times x_{i}) = g((\sum_{i = 1}^{n}w_{i,j} \times x_{i}) - w_{0,j}) finkitxmlcodelatexdvpChaque neurone de la couche donnera donc une sortie. Une utilisation courante est que chaque neurone de la couche représente une classe. Pour un exemple X donné, on obtient la classe de cet exemple en prenant la plus grande des p sorties. Essayons maintenant d'approfondir ce modèle.
IV-1. Modélisation Matricielle▲
Avec la notation que nous avons définie pour les poids, on obtient ainsi une matrice W = (wi,j)(i,j) / 1 <= i <= n et 1 <= j <= p où le coefficient ligne i colonne j représente le coefficient liant la i-ème information au p-ème neurone. Si on représente par A = (aj)1 <= j <= p la liste des p sorties du réseau de neurone, on obtient l'équation matricielle suivante, en adaptant la fonction de transfert à notre nouvelle modélisation : on définit une nouvelle fonction g qui prend l'image d'un vecteur en calculant l'image de chacune de ses composantes, et retourne un vecteur dont les composantes sont les images des composantes de départ.
kitxmlcodelatexdvpA = g(^{t}W \times X )finkitxmlcodelatexdvpCette modélisation n'est pas fréquemment utilisée mais représenter un réseau de neurones monocouche par une matrice permet d'avoir une autre vision du problème.
IV-2. Evaluation : RdN(X)▲
L'évaluation d'un exemple X = (xi)1 <= i <= n par un réseau de neurones donne un vecteur à p composantes. On définit la notation suivante.
kitxmlcodelatexdvpRdN(X) = g(^{t}W \times X)finkitxmlcodelatexdvpoù RdN(X) est un vecteur à p composantes, W une matrice à n lignes et p colonnes et X le vecteur dont chacune des n composantes représente une information d'entrée.
IV-3. Les différents types de perceptrons▲
Il existe 2 types de perceptrons : les perceptrons feed-forward et les perceptrons récurrents. Les perceptrons récurrents sont ceux qui alimentent leurs entrées avec leurs sorties, alors que les perceptrons feed-forward non.
IV-4. Séparation linéaire et conditions d'approximabilité▲
Pour un perceptron dont les fonctions de transferts sont toutes la fonction seuil (perceptron à seuil), en dimension 2, comme nous l'avons vu plus haut, on peut parfois tracer une droite telle que d'un côté de la droite, les points appartiennent à une première classe et de l'autre côté ils appartiennent à une seconde classe. Cette notion de séparation est généralisée. Pour un perceptron à p neurones, on parle de séparation de l'espace par un hyperplan de cet espace. Toutefois, on ne peut pas toujours avoir un hyerplan qui sépare l'espace en 2 parties, dans les cas où la fonction qu'on veut approcher est plus complexe.
Dans le cas où l'on peut séparer l'espace avec un hyperplan, on dit que la fonction à approcher est linéairement séparable.
En général, les perceptrons à seuil ne permettent de représenter que des fonctions linéairement séparables. De même, les perceptrons à sigmoïde sont assez limités, à la seule différence qu'ils représentent une séparation linéaire un peu plus douce.
IV-5. Comment choisir les poids ?▲
Malgré cette limitation, les perceptrons à seuil ont une propriété intéressante qui est celle que nous allons aborder dans la section suivante : il existe un (en fait plusieurs) algorithme(s) qui permet(tent) à un perceptron d'adapter ses poids à un ensemble d'exemples de sorte à obtenir pour cet ensemble la classification attendue. Ainsi, si l'ensemble d'exemples est assez vaste (les exemples sont assez variés), on pourra obtenir un perceptron qui donnera des résultats convenables pour des exemples non rencontrés.
V. Apprentissage simple du perceptron : méthode du gradient et algorithme de Widrow-Hoff▲
Il y a deux algorithmes, principalement, pour "faire apprendre" à un réseau de neurones monocouche. Le premier est la méthode simple et se nomme la descente de gradient. L'autre, un peu plus efficace généralement, se nomme algorithme de Widrow-Hoff, du nom des deux scientifiques qui ont élaboré cette technique.
Les deux méthodes consistent à comparer le résultat qui était attendu pour les exemples puis à minimiser l'erreur commise sur les exemples. Toutefois, il existe bien sûr une nuance entre les deux méthodes, qui va être expliquée plus loin.
Nous allons, pour chacune des méthodes, étudier la correction des poids concernant seulement l'un des neurones. Il suffira d'appliquer successivement la méthode de votre choix à chacun des neurones du réseau monocouche.
V-1. Apprentissage par descente de gradient▲
Pour comprendre cette méthode d'apprentissage, il faut définir l'erreur quadratique E. Si l'on est en présence de N exemples, alors pour 1 <= k <= N, notons (Xk,yk) le couple exemple - sortie attendue, où Xk = (xi)1 <= i <= n est le vecteur dont les coordonnées sont les n informations d'entrée de l'exemple et où yk est la sortie attendue (la sortie "vraie") pour cet exemple-là de la part de notre neurone. Enfin, on note sk la sortie obtenue pour le k-ème exemple avec les poids actuels. Alors, l'erreur quadratique est définie comme suit.
kitxmlcodelatexdvpE = \frac{1}{2} \sum_{k = 1}^{N}(y_{k} - s_{k})^{2}finkitxmlcodelatexdvpOn voit donc que l'erreur est nulle si le réseau de neurones ne se trompe sur aucun des exemples, c'est à dire s'il parvient à calculer la bonne sortie (par exemple classifier) pour chacun des exemples correctement. C'est rarement le cas car souvent on démarre avec des poids tirés aléatoirement. Il s'agit donc de minimiser, pour un ensemble de N exemples donné, cette erreur quadratique. Je n'ai pas jugé nécessaire de vous présenter en milieu de ce cours le calcul qui permet d'obtenir une minimisation de l'erreur quadratique. Toutefois, le résultat étant très important, la démonstration est disponible en annexe de cet article. On obtient la variation à appliquer à chaque poids afin de classifier au mieux (parfaitement, dans le meilleur des cas) chacun des N exemples.
On va noter kitxmlcodeinlinelatexdvp\alphafinkitxmlcodeinlinelatexdvp un nombre réel auquel on donne le nom de taux d'apprentissage. C'est nous qui devons lui donner une valeur lors de la mise en pratique de l'apprentissage. Comme nous ne considérons qu'un neurone à la fois, on va noter wi le poids reliant la i-ème information à notre neurone.
La méthode de descente du gradient consiste en fait à effectuer les actions suivantes :
- Créer n variables dwi, pour 1 <= i <= n, égales à 0
- Prendre un exemple ek, pour 1 <= k <= N
- Calculer la sortie obtenue avec les poids actuels, notée sk (1)
- Rajouter à dwi, pour tout 1 <= i <= n, le nombre kitxmlcodeinlinelatexdvp\alpha (y_{k} - s_{k}) x_{i}finkitxmlcodeinlinelatexdvp (2)
- Réitérer (1) et (2) sur chacun des exemples
- Pour 1 <= i <= n, remplacer wi par wi + dwi
Voici donc l'algorithme d'apprentissage par descente du gradient, appliqué à un seul neurone, qu'il faudra donc répéter sur chacun des neurones.
Entrée : n poids reliant les n informations à notre neurone ayant des valeurs quelconques
N exemples (X_k, yk) où X_k est un vecteur à n composantes x_i,
chacune représentant une information de cet exemple
Sortie : les n poids modifiés
POUR 1 <= i <= n
dw_i = 0
FIN POUR
POUR TOUT exemple e = (Xk, yk)
Calculer la sortie sk du neurone
POUR 1 <= i <= n
di = dw_i + alpha*(yk - sk)*x_i
FIN POUR
FIN POUR
POUR 1 <= i <= n
w_i = w_i + dw_i
FIN POURAfin d'obtenir de bons résultats, il faudra passer plusieurs fois les exemples à chaque neurone, de sorte que les poids convergent vers des poids "idéaux". Le problème avec cette méthode est que l'on corrige sur la globalité des exemples, ce qui fait que le réseau ne s'adaptera aux exemples qu'après un certain moment. Il y a une autre méthode qui permet de corriger sur chacun des exemples, et qui se nomme méthode d'apprentissage de Widrow-Hoff.
V-2. Apprentissage par l'algorithme de Widrow-Hoff▲
L'algorithme de Widrow-Hoff, ou encore "la règle delta", n'est en fait qu'une variante de l'algorithme précédent. Je vais détailler ceci.
Comme nous l'avons vu dans l'algorithme précédent, on engrange les erreurs commises sur chaque exemple puis pour terminer on corrige le poids, et ce pour chaque poids. Vous ressentez probablement cette méthode comme assez "grossière", dans le sens où elle n'est pas très précise et met beaucoup de temps avant de tendre vers le bon coefficient. On ressent le fait qu'elle ne corrige qu'un petit peu alors qu'elle pourrait corriger beaucoup mieux pour chaque exemple. Et c'est là que l'algorithme de Widrow-Hoff intervient. En effet, la méthode élaborée par Widrow et Hoff consiste à modifier les poids après chaque exemple, et non pas après que tous les exemples aient défilé. Ceci va donc minimiser l'erreur de manière précise, et ce sur chaque exemple. Instinctivement, on constate bien que le réseau de neurones va s'améliorer nettement mieux et va tendre bien plus rapidement à classifier parfaitement (ou presque) chacun des exemples, bien que des méthodes plus efficaces encore existent. Voici donc l'algorithme de Widrow-Hoff.
Entrée : n poids reliant les n informations à notre neurone ayant des valeurs quelconques
N exemples (X_k, yk) où X_k est un vecteur à n composantes x_i,
chacune représentant une information de cet exemple
Le taux d'apprentissage alpha
Sortie : les n poids modifiés
POUR TOUT exemple = (Xk,yk)
Calculer la sortie sk du neurone
POUR 1 <= i <= n
w_i = w_i + alpha*(yk - sk)*x_i
FIN POUR
FIN POURCette méthode est bien sûr plus efficace, comme dit précédemment, mais l'algorithme est plus simple également ! Je vous invite donc à tester tout d'abord cet algorithme dans des cas assez simples, comme les fonctions booléennes ainsi que tout autre exemple de ce genre auquel vous pourriez penser.
Appliquer plusieurs fois cet algorithme permettra d'affiner la correction d'erreur et d'obtenir un réseau de neurones de plus en plus performant. Attention toutefois, car l'appliquer un trop grand nombre de fois mènerait à ce que l'on appelle "l'overfitting" (sur-apprentissage), c'est à dire que votre réseau devient très performant sur les exemples utilisés pour l'apprentissage, mais ne parvient peu ou pas à généraliser pour des informations quelconques.
VI. Les types de réseaux de neurones▲
Il s'agit de généraliser ce qui a été vu en 4.3. Un réseau de neurones est simplement un ensemble de neurones liés entre eux, le poids étant partie intégrante de cette liaison. La façon de lier un neurone à un autre est de prendre la sortie de ce premier, d'affecter un poids à sa valeur et de rejoindre une entrée d'un autre neurone, comme nous l'avons déjà vu.
Les réseaux de neurones feed-forward sont des réseaux où les neurones ne sont connectés que dans un sens, le sens orienté de l'entrée vers la sortie. Les réseaux de neurones récurrents sont des réseaux où les neurones de sortie par exemple peuvent voir leur sortie utilisée comme entrée d'un neurone d'une couche précédente (nous verrons ce que sont les couches) ou de la même couche. Par conséquent, instinctivement il est évident que ce modèle est bien plus compliqué. Comme l'indique le titre de cet article, ce n'est pas ce modèle qui est étudié dans le cas d'un réseaux de neurones à plusieurs couches.
VII. Perceptron multicouche▲
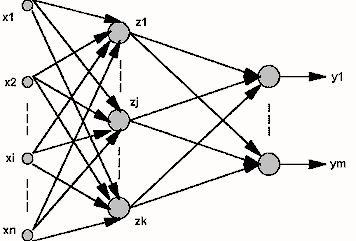
Nous avons précédemment étudié les perceptrons (réseaux monocouche) et nous avons vu que les neurones de sortie étaient chacun connectés aux mêmes informations. Nous les avons perçus comme une couche (alignés verticalement). Ainsi, une couche est constituée de neurones étant connectés aux mêmes informations mais n'étant pas connectés entre eux. Il s'agit maintenant de généraliser le perceptron. On peut ainsi disposer les neurones en plusieurs couches. Ainsi les informations en entrée sont connectées à tous les neurones de la première couche, tous les neurones de la première couche sont connectés à tous les neurones de la seconde couche, et ainsi de suite jusqu'à la dernière couche, appelée couche de sortie. Toutes les couches exceptée la couche de sortie sont considérées comme "couches cachées". Toutefois, n'ayez crainte : il a été prouvé que dans la plupart des cas, un réseau à 2 couches (informations -> une couche -> couche de sortie) où chaque neurone de la couche cachée a comme fonction d'activation la fonction sigmoïde et chaque neurone de la couche de sortie a comme fonction d'activation une fonction linéaire permet d'approximer une fonction continue. Il s'agit du Théorème de Cybenko. Pour des fonctions discontinues, nous n'avons aucune garantie.
Du fait du résultat précédent, nous allons restreindre notre étude aux réseaux neuronaux à une seule couche cachée. La couche cachée permet plus d'interaction et instinctivement, on est conscient que notre réseau de neurone pourra apprendre des "fonctions" plus complexes en rajoutant une couche. Le fonctionnement n'est pas pour autant complexe. On a toujours le choix de la fonction d'activation, et l'évaluation de la sortie d'un neurone se déroule de la même manière. La seule différence est que la sortie d'un neurone de la couche cachée sera l'une des informations d'entrées des neurones de la couche de sortie.
VII-1. Evaluation : RdN(X)▲
Il y a par rapport au perceptron monocouche une étape supplémentaire lors de l'évaluation de la sortie du réseau de neurone. On obtient ainsi une matrice des poids pour passer des informations à la couche cachée, et une autre matrice de poids pour passer de la couche cachée à la couche de sortie. Ensuite, cela revient au même que pour le réseau monocouche.
VII-2. Dimensionner un perceptron multicouches▲
Dimensionner signifie ici déterminer le nombre de neurones de chacune des deux couches. Pour la couche de sortie, cela dépend de la nature du résultat que vous attendez. Si vous avez besoin de n nombres en sortie, il vous faudra n neurones sur la couche de sortie, comme pour le perceptron monocouche. Pour la couche cachée, les choses sont beaucoup moins simples. Il n'existe aucune loi, aucune règle, aucun théorème qui permettrait de déterminer le nombre de neurones à placer dans la couche cachée pour avoir un réseau de neurones optimal. La méthode pour s'en rapprocher est d'essayer "au hasard" plusieurs nombres de neurones en couche cachée jusqu'à avoir des résultats les plus probants possibles après l'apprentissage. Il existe toutefois des résultats concernant certains types de fonctions que l'on souhaite approcher. Malheureusement, aucun de ces résultats n'est pour le moment assez générique pour être exploité dans les cas courants.
Nous ne nous attardons pas sur la présentation et l'explication du fonctionnement du perceptron multicouches étant donné qu'il fonctionne de manière analogue au perceptron monocouche. C'est pourquoi nous allons maintenant nous pencher sur l'apprentissage du perceptron multicouches.
VIII. Apprentissage du perceptron multicouches▲
De la même manière que le perceptron monocouche, le perceptron multicouche est lui aussi capable d'apprentissage. En effet, il existe également un algorithme permettant de corriger les poids vis à vis d'un ensemble d'exemples donnés. Cet algorithme est appelé algorithme de rétro-propagation du gradient.
Cet algorithme utilise la même règle de modification des poids ("delta rule") que l'algorithme de Widrow-Hoff. L'algorithme va être donné dans sa version la plus générale, c'est à dire avec plusieurs couches cachées. On notera g la fonction d'activation. Une démonstration de l'efficacité de cet algorithme exige de la fonction d'activation qu'elle soit indéfiniment dérivable. On notera si la sortie du neurone i de la couche de sortie et yi la sortie attendue pour ce même neurone. Enfin, pour des neurones d'une couche cachée, on notera oi la sortie calculée du neurone.
Entrée : un exemple, sous la forme (vecteur_x,vecteur_y);
epsilon le taux d'apprentissage
un Perceptron MultiCouches avec q-1 couches cachées C1, ..., Cq-1,
une couche de sortie Cq.
Répéter
Prendre un exemple (vecteur_x,vecteur_y) et calculer g(vecteur_x)
Pour toute cellule de sortie i di <- si(1-si)(yi-si) finPour
Pour chaque couche de q-1 à 1
Pour chaque cellule i de la couche courante
di = oi(1-oi) * Somme [pour k appartenant aux indices des neurones
prenant en entrée la sortie du neurone i] de dk*w_ki
finPour
finPour
Pour tout poids w_ij <- w_ij + epsilon*di*x_ij finPour
finRépéterLa variable "di" apparaît deux fois dans le code. Il s'agit de deux variables différentes, car en fait on suppose que les neurones sont numérotés de sorte que l'on puisse associer à un identifiant un neurone et réciproquement. Par conséquent, le 'i' de "di" identifie un neurone et ainsi on peut effectuer la dernière boucle de manière uniforme sans différencier pour la couche de sortie et les couches cachées.
Voici quelques remarques sur cet algorithme.
- L'algorithme de rétroprogation du gradient est une extension de l'agorithme de Widrow-Hoff. En effet, dans les deux cas, les poids sont mis à jour à chaque présentation d'exemple et donc on tend à minimiser l'erreur calculée pour chaque exemple et pas l'erreur globale.
- La méthode donne de bons résultats pratiques. Dans la plupart des cas, on rencontre peu de problèmes dûs aux minima locaux, mais il y en a. Toutefois, il est moins performant que d'autres algorithmes de propagation d'erreur : il tend moins rapidement vers des poids plus ou moins optimaux.
- Il n'y a pas de condition d'arrêt pour le REPETER. C'est à vous de fixer le critère. On peut par exemple répéter cela jusqu'à ce que l'erreur sur chaque exemple descende en dessous d'un certain nombre.
- Le choix de l'architecture initiale du réseau reste un problème difficile. Ce choix peut être fait par l'expérience. Des méthodes dites "auto-constructives" existent : il s'agit d'ajouter des neurones au cours de l'apprentissage pour que l'apprentissage se fasse bien. Mais ces méthodes rencontrent souvent le problème de "sur-apprentissage", mentionné dans la section 5.2. L'architecture peut aussi être choisie à l'aide de méthodes basées sur les algorithmes génétiques.
IX. Conclusion▲
Il y a principalement deux facteurs qui influent sur l'apprentissage. Ce sont la qualité de l'échantillonage d'apprentissage(les exemples qui constituent la base d'apprentissage) et la diversité des valeurs. En effet, le réseau de neurones généralisera mieux (aura plus de chances de répondre correctement en lui donnat en entrée des informations non présentes dans les exemples d'apprentissage) si la qualité de l'échantillonage est meilleure et si les données des exemples d'apprentissage sont variées. Intuitivement, on est conscient que s'il sait répondre correctement pour un nombre fini de situations les plus diverses, il sera alors plus proche de ce que l'on veut dans un situation nouvelle.
Nous avons présenté la théorie des réseaux de neurones artificiels feed-forward (c'est à dire ne comportant pas de connexions vers des couches précédentes). Il existe des structures de réseaux de neurones beaucoup plus complexes. Si cela vous intéresse, renseignez-vous sur les réseaux récurrents et les cartes de Kohonen, par exemple. Pour toute question, n'hésitez pas à consulter et poster sur le forum Intelligence Artificielle de DeveloppezForum I.A de Developpez.
X. Remerciements▲
Je tiens à remercier l'équipe Algorithmes de Developpez pour m'avoir aidé lors de la rédaction de cet article, en particulier pseudocode (Xavier Philippeau)Profil de pseudocode, Eusebius (Guillaume Piolle)Profil d'Eusebius, khayyam90 (Pierre Schwartz)Profil de khayyam90, PRomu@ld (Romuald Perrot)Profil de PRomu@ld et TheLeadingEdgeProfil de TheLeadingEdge pour leur relecture attentive de l'article et pour leurs suggestions, ce qui n'est pas rien.
Si une erreur s'est glissée dans l'article, n'hésitez pas à me contacter par MP ou par mail pour me le signaler.
XI. Annexe : Démonstration de la règle delta▲
La démonstration va être effectuée dans le cas d'un perceptron à une couche cachée. Nous allons utiliser la définition de l'erreur quadratique sur un seul exemple dont nous avons parlé dans l'article.
kitxmlcodelatexdvpE = \frac{1}{2} \sum_{i}(y_{i} - s_{i})^{2}finkitxmlcodelatexdvpOn effectue la somme sur les neurones de la couche de sortie. De plus, pour terminer, nous noterons wk,j le poids reliant le k-ème neurone de la couche d'entrée au j-ème neurone de la couche cachée et wj,i le poids reliant le j-ème neurone de la couche cachée au i-ème neurone de la couche de sortie.
Pour obtenir le gradient par rapport à un poids wj,i donné dans la couche de sortie, il suffit de développer l'activation ai, puisque aucun autre terme de la sommation n'est affecté par wj,i
kitxmlcodelatexdvp\frac{\partial E}{\partial w_{j,i}} = - (y_{i} - a_{i})\frac{\partial a_{i}}{\partial w_{j,i}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - (y_{i} - a_{i})\frac{\partial g(in_{i})}{\partial w_{j,i}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - (y_{i} - a_{i})g'(in_{i})\frac{\partial in_{i}}{\partial w_{j,i}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - (y_{i} - a_{i})g'(in_{i})\frac{\partial }{\partial w_{j,i}}(\sum_{l} w_{l,i}a_{l})finkitxmlcodelatexdvp kitxmlcodelatexdvp= - (y_{i} - a_{i})g'(in_{i})a_{j} = - a_{j}\Delta_{i} finkitxmlcodelatexdvpoù kitxmlcodeinlinelatexdvp\Delta_{i}finkitxmlcodeinlinelatexdvp est le di dans la description des algorithmes.
De même, nous allons voir comment le gradient effectue la rétropropagation dans le réseau.
kitxmlcodelatexdvp\frac{\partial E}{\partial w_{k,j}} = - \sum_{i}(y_{i} - a_{i})\frac{\partial a_{i}}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}(y_{i} - a_{i})\frac{\partial g(in_{i})}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}(y_{i} - a_{i})g'(in_{i})\frac{\partial in_{i}}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}\frac{\partial }{\partial w_{k,j}}(\sum_{j} w_{j,i}a_{j})finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}w_{j,i}\frac{\partial a_{j}}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}w_{j,i}\frac{\partial g(in_{j})}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}w_{j,i}g'(in_{j})\frac{\partial in_{j}}{\partial w_{k,j}}finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}w_{j,i}g'(in_{j})\frac{\partial }{\partial w_{k,j}}(\sum_{l}w_{l,j}a_{l})finkitxmlcodelatexdvp kitxmlcodelatexdvp= - \sum_{i}\Delta_{i}w_{j,i}g'(in_{j})a_{k} = -a_{k}\Delta_{j} finkitxmlcodelatexdvpOù kitxmlcodeinlinelatexdvp\Delta_{j}finkitxmlcodeinlinelatexdvp représente une partie des di dans les algorithmes : ceux de la couche cachée.





